Let’s TAC™ About It: Homomorphic Encryption Algorithms on TAC™ (HEAT)

For the sixth installment of our blog series, we will cover homomorphic encryption algorithms on TAC™, known as HEAT. So, are you ready to TAC™ about it?

It’s standard practice to encrypt data at rest (e.g., data in a database) and in transit (e.g., data sent over the internet). When an analyst has to work with data, however, the data is usually unencrypted to perform any calculation. Homomorphic encryption (HE) is cryptography that holds the promise of allowing computations on data while it remains encrypted. 

Despite the increasing need for data security and privacy, HE is not widely used. There are at least two barriers to adoption:

• Impracticality: NIST-compliant encryption schemes that power widely-used protocols such as RSA have well-known properties that make it possible to perform a subset of arithmetic operations on encrypted numbers. Many of these methods, however, require brute-force computation that limits their ability to add large numbers.
• Lack of standardization: To overcome the limitations of NIST-compliant encryption schemes, many new HE protocols have been developed to perform operations on larger numbers with some powerful optimizations. Unfortunately, none have been proven reliable enough to be standardized. Even large projects such as Microsoft SEAL have recognized security challenges.

VIA’s HE algorithm overcomes both these barriers for addition. Our protocol uses NIST-compliant standard elliptic curve cryptography (ECC) algorithms to sum arbitrarily large numbers. The key innovation is to represent integers in a base of 2ⁿ and sum the numbers for each column in separate batches up to an overflow limit of 2³². This resulting number (a vector of numbers less than 2³²) can thus be decoded using standard brute-force decoding algorithms. 

To avoid overflow limits, the protocol is limited to summing 2^(32-n) numbers at a time. If, however, there is a need to sum more than 2^(32-n) at a time, we can increase the overflow limit by increasing computation power available for decoding. We distribute the computation to multiple machines to execute the decoding in parallel. In practice, HE is normally used on numbers that are already aggregated, so the 2^(32-n) number limit is not a significant barrier. 

As an example, imagine a decrypting system that could only handle numbers up to 1,000 in base 10. How would you add the numbers, 236 and 56,798? While such a decrypting system can only handle numbers up to 1,000, we are not hampered by this limitation. The number 236 can be represented as a vector of (6,3,2,0,0). The number 56,798 is represented as (8,9,7,6,5). Adding the two numbers, we get (14, 12, 9, 6, 5). We can decode each of the components of that vector because they are all less than 1,000. We can then reexpress this result as (4,3,0,7,5) and finally decode this as 57,034. With this approach, we can add up to 100 numbers at a time and be sure that none of the individual columns exceed 1,000 and thus our cryptosystem will work.

What if we need to add 200 numbers? In this case, we can choose a small base (e.g., from 2¹⁶ to 2⁴) and raise the limit beyond 1,000 by distributing the decoding in parallel. The size of the base determines the amount of brute-force computation required. By breaking the addition into a series of smaller problems, it now becomes possible to use standardized encryption algorithms and brute-force computation to solve the problem. We also leverage existing standards to make it practical to perform arbitrarily complex sum operations. 

VIA has incorporated this HE addition algorithm into its TAC™ platform, known as Homomorphic Encryption Algorithm on TAC™ or HEAT.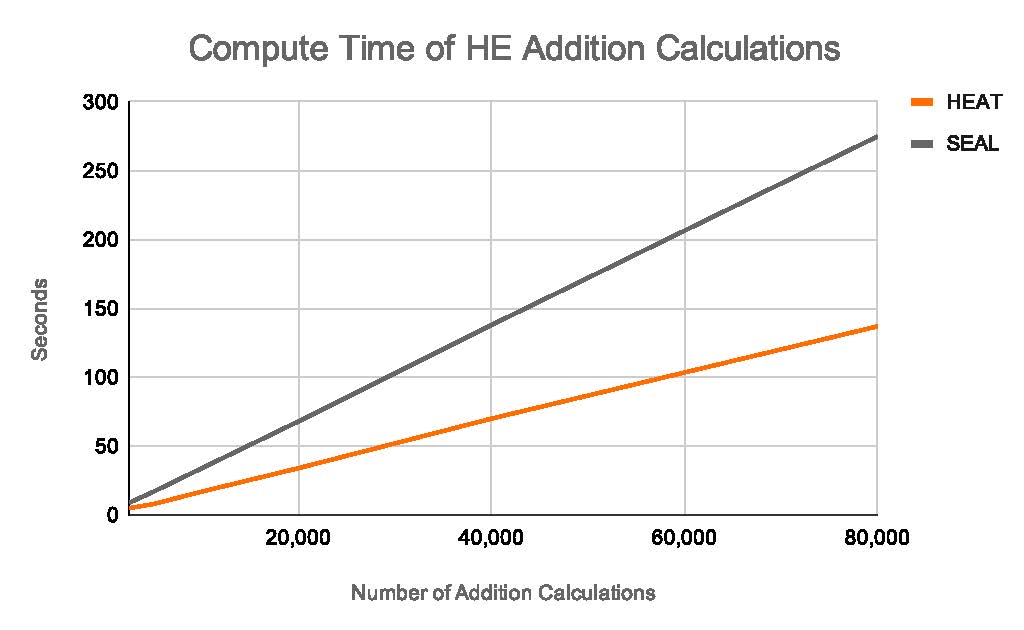

To benchmark the system, we compared execution times for HEAT versus Microsoft SEAL, a popular open source HE library. The simple benchmark consists of recording the execution time to encrypt, add, and decrypt up to 80,000 integers. The cryptographic parameters for the ECC were chosen to match the same level of protection as SEAL.

The graph above shows that HEAT is roughly twice as fast as SEAL.

At VIA, we’re excited to have found a “no-tradeoff” solution for HE addition that has wide applications. We are already using HEAT to enable encrypted benchmarking of data across utilities as part of our GDAC™ program. We are also looking into using HEAT for training a federated deep learning model.

HE is a rapidly developing field. VIA is increasing its dedicated resources to improve its HE implementation including exploring lattice cryptography to meet post-quantum computing requirements and extending HEAT to enable homomorphic multiplication.